Key to Nuclear Models

Color-Coded Quarks

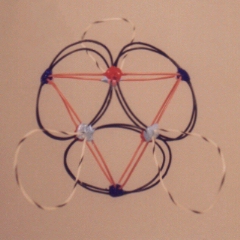The models are color coded for easy identification of quarks. Up quarks are always shown in red. Down quarks are typically dark blue, however on some of the models you may also notice light blue quarks where vector bosons are pinned. (I did not follow this convention on all of the models, the N4-22P, P4-21P, and one of the N1 examples are the only exceptions.) A quark with a pinned string is actually an Up quark, but the pinning of a vector boson allows the Up quark to emulate a Down quark in the nuclear shell. Sharp observers will also notice that many of the models have two-tone Down quarks... that is, they are blue on the outer surface, but pink or red on the inner surface. This is not an error, it is indicative of the two charge surfaces of a down quark. (I only did this on some of the models.) The theory underlying the nuclear models suggest that all quarks have two surfaces manifesting charge mirrors, in the Up quark, both charge mirrors are positive, but the Down quark has both a positive and negative charge mirror. I believe the negative mirror usually appears on the exterior surface of a shell, while the positive mirror faces the interior of the shell. I suspect this posture is due to charge influences nearby, so I would consider it possible that there could be circumstances which would flip the posture of the Down quarks' charge mirrors.

For a "bogus" down quark (an Up quark with a pinned vector boson) the pinned vector boson contributes the negative-surfaced charge mirror. The description of how these charge mirrors are construed to manifest the charge force is out of the scope of this web site at this time. It should be adequate for testing purposes to simply know that a (bogus) down quark has an outer negative surface, and an inner positive surface, the net charge being equivalent to -1/3. I am not entirely certain if the standard down quark has two disparate surfaces like the (bogus) down quark, or if it has two negative surfaces. I tend to favor disparate surfaces as it may provide an explanation for the structure of mesons as a back to front stacking of quarks of the same variety. There is another very significant reason why I favor this model, but since I'm not yet prepared to reveal it, I'll focus on the meson argument. Quark-anti-quark pairings might not work to explain mesons in this model, as antiquarks are made of colliding anti-hadron strings. Pairing a quark with an anti-quark should lead to the immediate annihilation of both in a shower of photons. I guess the lifetime of mesons is pretty short, and this is uncertain ground for me, as I have focused almost entirely on stable, long-lived particles. What I'm saying is, my concept of meson structure may be based more on ignorance than on fact, so don't toss the quark-anti-quark meson model out the window just yet.

What is a Quark?

A quark, in this theory, is a collision cell of light strings. The light strings intermix in this collision cell, and form a very special pair of mirror-like surfaces that support the phenomenon of charge. The collision cell (quark) is conserving several properties of the colliding strings, and is a quasi-particle, or constituent particle in a larger structure. The larger particle structure is generally conserved by the laws of baryon number or lepton number conservation. A particle generally requires quarks in multiples of three for stability, possibly as a function of conservation of integer charge. These conservation laws govern the cosmological existence of stable elementary particles, and should be construed at this level as constraints imposed by the geometry of space-time for elementary particles, of which quarks are subordinate entities.

Only three types of quarks are dealt with in this theory, Up, Down, and an Up quark which pins an external string to emulate a Down quark, called the "Bogus Down" quark. The bogus down quark is the most important in confirming the nuclear shell models, bogus down quarks are the pinning sites of external strings which form the lobes of electron orbitals. The Charm, Strange, Top and Bottom quarks are collision cells sporting additional strings, generally found only in high energy investigations as short-lived entities, and I have not bothered to explore them fully as I doubt their immediate usefulness to chemists. What I have provided, if it proves to be correct, represents some extremely useful information to chemists. If the charge structure and electron configurations of nuclei can be fully and accurately modeled, computers would be capable of modeling any chemical compound, or design new materials at the whim of the chemist. The days of experimentally sloshing reagents in test tubes might come to an end.

Loop Scale

There is also some data associated with the models which requires explanation. The values for "L1, L2, etc..." are Loop Values. If you were to cut the loop and measure its linear dimension, it would be this long. Well, actually, my models are 1/2 the given scale. When I first started building the models from wire I used 18 gauge solid wire, making the models large enough for classroom demonstration. (The very first models were drawn on balloons, then ping pong balls.) Since then the models have been getting unmanageably large, so I went with 22 gauge solid wire and cut all Loop dimensions by half. If you build the models, use an engineering rule with a "20's" scale to measure the wires. The 20's scale will let you make a direct measurement of the wire as given in the description, yet still produce reasonably sized models.

Scaling String by Mass of the Nuclear Shells

As long as I'm talking about the scale of the models, I should point out that the scale of these models are based on an assumption I know to be false, but there is a sound reason for doing so. The false assumption is that the energy of the string is proportional to its linear dimension. This is not entirely false, it just doesn't go far enough. If the frequency of the nuclear strings were a constant, this assumption would be true, but the frequency of the nuclear strings has a significant impact on their length. I once suspected that the nuclear strings in the various shells of a single nucleus would all be at the same frequency. That assumption has proven to be false, the nucleus is more flexible than I had imagined. I believe chemists have found a P3 shell ¹¹Li (lithium) with a halo of neutrons around an ⁸Li or ⁹Li core. This is an excellent candidate for a shell system running shells at very different nuclear frequencies. It has also become apparent in the course of working with the geometry that neutron shells (which typically have more string than the proton shells) generally take the inner position. A shift in frequency is the most obvious way of expanding and shrinking nuclear shells, and the highest frequency shells should be at the bottom of the stack (interior of the nucleus). As a rule of thumb, if you double the frequency of a nuclear string, you halve its length. It also appears as though the local energy-density of the space-time medium has much to do with the quiescent frequency of the nuclear strings immersed in that medium. As you penetrate into the nucleus, the energy-density gradient ramps up quickly, and the string frequencies appear to be coupled to that gradient.

(Note: The atomic spectrum of an atom may be a harmonic of a nuclear string's frequency. A pinned vector boson probably bears a harmonic relationship to the nuclear string frequency of the particular nuclear shell it is pinned to.)

Loop Equations and Snap Point Equations

I've found these two descriptive equations of the models coupled with the pictures to be an adequate description of the models for the purpose of reproducing them. The coefficients in the Loop Equation tell you how many loops of each size will be required. The solution to the loop equation is always a multiple of 51 inches (arbitrarily chosen), and is representative of the mass of the particle. The Snap Point Equation describes the number of string crossings in the model. Every Down quark requires 4 snap points, corresponding to the intersection of four strings which characterize a Down quark. Every Up quark requires three snap points. By calculating the number of down quarks x4 plus the number of Up quarks x3 you arrive at the "Required Snap Points" (R.S.P.). If the nuclear geometry has less "Available Snap Points" (A.S.P.) than the shell requires, Pinned Vector Bosons (P.V.B.'s) must be added to make up the difference. A pinned vector boson contributes one snap point. The snap point equation has an influence on the loop equation in some models. If two nuclear strings have the same linear dimension (loop size) but a different number of snap points, they are characterized in the loop equation as a seperate entry.

Shell Naming Convention

I tried to give the shells descriptive names. These names take the form of P6-30PB, and N5-3(10)P. The first letter/number pair tells you if it is a proton (P) or neutron (N) shell, and the number tells you how many particles (protons or neutrons) are in the shell. (Multiply that number by three to find how many actual quarks are in the shell.) This number is followed by a dash to seperate it from the numbers which follow. The first digit tells you how many loop sizes are used to create the shell, in the case of P6-30PB that would be three, so you know from this that the loop equation will be a third degree equation. The next digit(s) indicate how many pinned vector bosons the model requires. In the case of N5-3(10)P there are 10 pinned vector bosons, and since there is more than one digit in this case, the number 10 has been bracketed. For P6-30PB there are no (0) pinned vector bosons, so a zero is indicated in this position. There may be one or more letters following the number, and this is what they mean:

P - A Polar Star Shell

S - Contains a Sinusoidal String

PS - A Polar Star Shell with a Sinusoidal String

CG - A special case indicating that the described shell represents the Core Geometry of the shell, no Filler Circlets or P.V.B.s are indicated, and thus it is not a complete solution, but merely the structural geometry on which multiple solutions may be modeled.

A, B, C, ... - More than one shell was found to have the same name by this naming convention, thus they must be further differentiated by a letter series. It probably would be smart to place this letter in brackets to avoid confusion, but I have not done so, as the situation has only arisen twice thus far.

So the name P6-30PB means it is a Proton Shell containing 6 protons that was built using three (3) different loop sizes, the geometry of which required zero (0) pinned vector bosons, and it represents a Polar Star solution. The "B" at the end tells you that there is another similar shell named P6-30PA.

Shell Stacking is the Key

Remember as you view various nuclear shells that you must stack proton and neutron shells to build the various isotopes. One of the great difficulties I have had with these models is that their physical construction does not permit me to easily stack the wire-frame models for detailed study of their charge distributions and vector properties. That is the purpose of this website. I am hoping to generate enough interest in nuclear geometry to spur some computer modeling of the structures, which would permit stacking the shells for detailed analysis and confirmation of the physical models. Interested computer programmers should examine the empirical laws of the geometry, realizing that I have not yet given a complete description of string properties.

Home
Chemistry Notes
Nuclear Shells
Empirical Laws
How to Build Them
Mensuration
Glossary