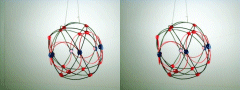
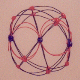
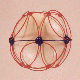
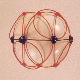
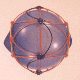
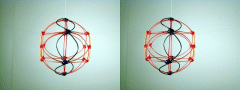
| A third degree solution set for P6. This one places all six down quarks
on an equatorial circlet. The P6-30PB shell stacks with N6-30P
to form an extremely stable complementary shell structure,
and I believe it represents the most likely solution for the principal nuclear isomer
of carbon 12. This complementary shell structure for C12 has highlighted a facet of
chemistry which has always mystified me, and finding this unexpected solution for C12
has caused me to revisit my assumptions on the matter, resulting in something of an
epiphany for me. It is a puzzle that I now intend to share with you.
 I once thought only inert gases would be characterized by complementary shells with no
P.V.B's, so I was quite surprised when I stumbled onto this rather mysterious solution
for C12. With this proton shell stacked on top of N6-30P the charge structure of the
resulting cation would be "dumbell" or "peanut" shaped. According to the chemistry texts,
C12 contributes four electrons to bonding. In the free state, one pair of electrons would
reside at either pole. In the bound state, such as in a buckyball, three electron pairs
(one of which is contributed by an adjacent C12) would locate at one pole 120 degrees
apart, while the opposite pole might harbor the third native pair, or be capable of
accepting an additional electron pair, by virtue of the resulting highly polarized
state of this nucleus. It all kind of depends on where the "s" orbital (non-valence) pair
are truly located. Since this is an extremely homogeneous charge structure for C12 by virtue
of the complementary nuclear shells, the two electrons presumed to form the "s" orbital may
actually be nestled in the nuclear interior. There should be plenty of room in there for
them, as well as strong positive charge currents off the underside of the neutron shell.
On the other hand, and more in line with conventional wisdom, the lack of P.V.B.s may
actually encourage electron pairs to hover more closely to the nuclear surface by permitting
them to avoid direct interaction with the charge jets emanating from the quarks on the
nuclear surface.
I once thought only inert gases would be characterized by complementary shells with no
P.V.B's, so I was quite surprised when I stumbled onto this rather mysterious solution
for C12. With this proton shell stacked on top of N6-30P the charge structure of the
resulting cation would be "dumbell" or "peanut" shaped. According to the chemistry texts,
C12 contributes four electrons to bonding. In the free state, one pair of electrons would
reside at either pole. In the bound state, such as in a buckyball, three electron pairs
(one of which is contributed by an adjacent C12) would locate at one pole 120 degrees
apart, while the opposite pole might harbor the third native pair, or be capable of
accepting an additional electron pair, by virtue of the resulting highly polarized
state of this nucleus. It all kind of depends on where the "s" orbital (non-valence) pair
are truly located. Since this is an extremely homogeneous charge structure for C12 by virtue
of the complementary nuclear shells, the two electrons presumed to form the "s" orbital may
actually be nestled in the nuclear interior. There should be plenty of room in there for
them, as well as strong positive charge currents off the underside of the neutron shell.
On the other hand, and more in line with conventional wisdom, the lack of P.V.B.s may
actually encourage electron pairs to hover more closely to the nuclear surface by permitting
them to avoid direct interaction with the charge jets emanating from the quarks on the
nuclear surface.
 I used to suspect electron pairs residing on P.V.B.s would form stronger bonds by virtue of
the P.V.B.'s themselves, but the action of the P.V.B.'s would tend to place the pinned
electrons within the direct influence of the negative nuclear charge jets, essentially pushing
them farther from the nuclear surface, resulting in a longer bond geometry and consequently a
weaker charge exchange between electrons and nuclei. Now this seems slightly mysterious, in
that the stacked shells for helium 4 should form a strong bond as well, but the answer may lie
in the mutual repulsion of the electron pairs. In Helium 4, there is only one electron pair,
and that pair may hover so close to the He4 nucleus, even encircling it, so that the nuclear
charge and the electron charge cancel quickly and very near the nuclear surface, making
helium 4 a very slippery atom. (Even more so if the electron pair takes up residence in the
nuclear interior, as then it would present no opportunity to form any sort of electron-mediated
bonds.) In the buckyball example of bound carbon 12, with three pairs of electrons mutually
attracted to one of the C12 poles, the mutual repulsion of the electron pairs may act to force
the electron pairs to hover higher above the nuclear surface, extending the charge structure
of the atom to more readily facilitate covalent bonds. But if that is the case, it should
force the "s" orbital pair to the opposite pole, permitting another covalent bond off of that
pole as well. I don't think that's what is happening though, which is one reason why I suspect
the "s" orbital pair may be hiding out in the nuclear interior.
I used to suspect electron pairs residing on P.V.B.s would form stronger bonds by virtue of
the P.V.B.'s themselves, but the action of the P.V.B.'s would tend to place the pinned
electrons within the direct influence of the negative nuclear charge jets, essentially pushing
them farther from the nuclear surface, resulting in a longer bond geometry and consequently a
weaker charge exchange between electrons and nuclei. Now this seems slightly mysterious, in
that the stacked shells for helium 4 should form a strong bond as well, but the answer may lie
in the mutual repulsion of the electron pairs. In Helium 4, there is only one electron pair,
and that pair may hover so close to the He4 nucleus, even encircling it, so that the nuclear
charge and the electron charge cancel quickly and very near the nuclear surface, making
helium 4 a very slippery atom. (Even more so if the electron pair takes up residence in the
nuclear interior, as then it would present no opportunity to form any sort of electron-mediated
bonds.) In the buckyball example of bound carbon 12, with three pairs of electrons mutually
attracted to one of the C12 poles, the mutual repulsion of the electron pairs may act to force
the electron pairs to hover higher above the nuclear surface, extending the charge structure
of the atom to more readily facilitate covalent bonds. But if that is the case, it should
force the "s" orbital pair to the opposite pole, permitting another covalent bond off of that
pole as well. I don't think that's what is happening though, which is one reason why I suspect
the "s" orbital pair may be hiding out in the nuclear interior.
 If this turns out to be true, then the strong nuclear force is considerably weaker
than old-style calculations would lead us to believe. That is because those calculations
are based on the electrostatic repulsion of the protons, which were assumed to be discrete
entities (like a cluster of grapes) repulsing each other from their surfaces. (Note 2008:
Well, um, at least I assume that's what they based them on, if not, they were based on the
binding energies, like how many million electron volts of energy it takes to knock a proton
or neutron out of the nucleus. I'll have to look into that. Sorry for the interruption.)
We can see with these shell structures that this "cluster of grapes" is not the case,
a proton shell is a composite of all the
protons in that shell, and the electrostatic repulsion from surface to surface of discrete
protons simply does not apply. Nuclear shells are more like delicately webbed soap bubbles
nestled in minimum energy configurations. This configuration of nuclear structure means that
there is, or can be a great deal of empty space in the interior of a nucleus, and if one or
more electron pairs take up residence there, then there is a significant reduction in the
electrostatic repulsion between opposite sides of the proton shells as the internal electrons
would cancel much of that effect. This would result in a reduction in the required strength
of the strong nuclear force to bind protons in the nucleus. Even the stacking of neutron
shells and proton shells is done in such a way so as to achieve the greatest neutralization
of the charge currents between adjacent quarks in upper and lower shells, and this too will
reduce the electrostatic repulsion between the combined protons in the proton shells.
Additionally, the theory underlying this string model suggests that the underside of both
up and down quarks act as positive charge sources, making the hollow nuclear interior a very
attractive environment for electrons, and it is almost inconceivable that electrons would not
find their way into that enormous, hollow, positively charged space. Another factor to consider
is that leptons and hadrons have structure in different domains in this theory... an electron
does not have to pass through the string geometry of a nuclear shell to get inside of it, as
those nuclear strings do not reside in lepton space where the electrons display their structure.
So yes, I think the non-valence electrons will often be found hanging out in the nuclear interior.
If this turns out to be true, then the strong nuclear force is considerably weaker
than old-style calculations would lead us to believe. That is because those calculations
are based on the electrostatic repulsion of the protons, which were assumed to be discrete
entities (like a cluster of grapes) repulsing each other from their surfaces. (Note 2008:
Well, um, at least I assume that's what they based them on, if not, they were based on the
binding energies, like how many million electron volts of energy it takes to knock a proton
or neutron out of the nucleus. I'll have to look into that. Sorry for the interruption.)
We can see with these shell structures that this "cluster of grapes" is not the case,
a proton shell is a composite of all the
protons in that shell, and the electrostatic repulsion from surface to surface of discrete
protons simply does not apply. Nuclear shells are more like delicately webbed soap bubbles
nestled in minimum energy configurations. This configuration of nuclear structure means that
there is, or can be a great deal of empty space in the interior of a nucleus, and if one or
more electron pairs take up residence there, then there is a significant reduction in the
electrostatic repulsion between opposite sides of the proton shells as the internal electrons
would cancel much of that effect. This would result in a reduction in the required strength
of the strong nuclear force to bind protons in the nucleus. Even the stacking of neutron
shells and proton shells is done in such a way so as to achieve the greatest neutralization
of the charge currents between adjacent quarks in upper and lower shells, and this too will
reduce the electrostatic repulsion between the combined protons in the proton shells.
Additionally, the theory underlying this string model suggests that the underside of both
up and down quarks act as positive charge sources, making the hollow nuclear interior a very
attractive environment for electrons, and it is almost inconceivable that electrons would not
find their way into that enormous, hollow, positively charged space. Another factor to consider
is that leptons and hadrons have structure in different domains in this theory... an electron
does not have to pass through the string geometry of a nuclear shell to get inside of it, as
those nuclear strings do not reside in lepton space where the electrons display their structure.
So yes, I think the non-valence electrons will often be found hanging out in the nuclear interior.
 Of course, at this point in time the idea of electrons locating themselves in the nuclear
interior is highly conjectural. To my knowledge I am currently the only supporter of this
belief. (For what its worth, I am currently the only supporter of nuclear geometry.) If
electrons do reside in nuclear interiors, it is quite possible that these
internalized electrons will construct shell geometries identical to the proton shells, but
residing in lepton space instead of hadron space. It is something to ponder. When all of these
contributing factors are taken into consideration, it seems as if the strong nuclear force
may not amount to much more than the familiar electromagnetic force and the electrostatic
interplay of charged surfaces. You can see, simply by looking at the stacked shell models,
that these shells are maintained by electrostatic forces, and if they turn out to be an
accurate description of the nucleus, then there is no strong nuclear force. For now I
will call this the "mystery of the "s" orbitals," and reserve further judgement. (For
reference to casual readers, "s" orbitals are typically characterized as tightly bound
spherical orbitals, encompassing the nucleus, whereas "p" orbitals are teardrop shaped lobes,
and overlapping "sp" orbitals are broad fan shaped orbitals, also referred to as hybridized
orbitals. An "orbital" is essentially a region in which a pair of electrons are located.)
Of course, at this point in time the idea of electrons locating themselves in the nuclear
interior is highly conjectural. To my knowledge I am currently the only supporter of this
belief. (For what its worth, I am currently the only supporter of nuclear geometry.) If
electrons do reside in nuclear interiors, it is quite possible that these
internalized electrons will construct shell geometries identical to the proton shells, but
residing in lepton space instead of hadron space. It is something to ponder. When all of these
contributing factors are taken into consideration, it seems as if the strong nuclear force
may not amount to much more than the familiar electromagnetic force and the electrostatic
interplay of charged surfaces. You can see, simply by looking at the stacked shell models,
that these shells are maintained by electrostatic forces, and if they turn out to be an
accurate description of the nucleus, then there is no strong nuclear force. For now I
will call this the "mystery of the "s" orbitals," and reserve further judgement. (For
reference to casual readers, "s" orbitals are typically characterized as tightly bound
spherical orbitals, encompassing the nucleus, whereas "p" orbitals are teardrop shaped lobes,
and overlapping "sp" orbitals are broad fan shaped orbitals, also referred to as hybridized
orbitals. An "orbital" is essentially a region in which a pair of electrons are located.)
NOTE, 03 MAR 2008: I'm fairly well convinced at this point in time that there is no strong nuclear
force, per se. I believe three classical influences are at work in binding the nucleus; the
electromagnetic force, represented by the strings, the electrostatic forces of charge courier
exchanges, and the Casimir effect operating between quarks stacked on top of each other in
adjacent nuclear shells. It is becoming increasingly obvious to me that all non-valence electrons
are building interstitial shells within the hadron shells. The repulsive effects of the positive
charges of the quarks in the nuclear shells are greatly cancelled by interleaving electron shells.
However, this raises an interesting question... do these electron shells (composed of lepton string)
pin strings, or is the geometry more restrictive for electron shells interleaved with proton and
neutron shells? (The rules for geometering electron shells from lepton string are almost identical
to the rules for constructing proton shells, the only real difference being in the way external strings
are pinned.) I now suspect that "partons" found in nuclear collision data may represent collisions
with leptonic down quarks in intelaced nuclear electron shells. (I previously attributed partons to
string-string collisions, however discovering that my model describes another class of hard point-like
objects swimming in the nuclear sea, this seems the more likely candidate.)
|